Fig.1: larger. Klong
| Prev: Introduction | Content | Next: Basic Statistical Functions |
A data set is stored in a Klong vector. There are various ways to create data sets. Key them in:
[30 28 31 30 31 30 31 31 30 31 30 31]
|
Use the Enumerate or Expand operators:
5+&10
|
Or create a data set following a
probability distribution
with
dist. For instance, the following program creates a data set
of
normally distributed
data:
&dist(ndf;7;[-2 2])
|
The dist function itself returns a
frequency distribution
which can then be expanded to a data set using Expand:
dist(ndf;7;[-2 2])
|
The parameters of
dist are the
probability density function
(PDF) of the
desired distribution, the number of different data points to generate,
and the desired range of the PDF. The above example creates 7 standard
normally distributed data points (using the ndf function)
from −2σ to +2σ.
A data set can be converted (back) to a frequency distribution using the idiom Size-Each Group:
#'=[0 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 4 4 5 5 5 6]
|
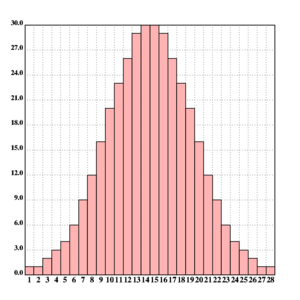
Larger data sets are best visualized using the interactive plotter interface. For instance, the following program creates the histogram plot in fig.1 from a frequency distribution.
X::&dist(ndf;30;[-3 3])
v.bar(#'=X)
|
The v.bar function sets up a grid and plots a data
set as a bar graph. The Klong program linked below the image does not
use the interactive interface, but similar instructions for batch
plotting.
A normally distributed random
error
can be added to a data set by
using the err function. For instance:
&20
|
The first parameter of err specifies the number of
distinct error values, taken from the interval −0.5≤x≤0.5
with equal space between them. The lowest value is always −0.5
and the highest value is 0.5. The second parameter is multiplied with
the error values, so the above example generates the error values
{−2, −1, 0, +1, +2}.
An x/y set or paired set or map is represented by a vector of tuples. It is normally used to pair the values of two random variables that may be correlated or not. Like a data set it can be keyed in or created using various operators and functions. A data set can be turned into an x/y set by pairing each value in the set with some other value, e.g.:
[3 6 7 13 17 17 21]
|
An x/y set can be divided into two separate data sets using the First-Each and (At-one)-Each idioms:
XY::[[1 3] [2 6] [3 7] [4 13] [5 17] [6 17] [7 21]]
*'XY
|
Larger x/y sets are best visualized as scatter plots. For example, the program
v.scatter2((!30),'err(20;20;0.5*!30))
|
will display a scatter plot like the one shown in fig.2. Of course, the actual values plotted by the program may differ from those in the figure due to the random error added.
| Prev: Introduction | Content | Next: Basic Statistical Functions |